Authors:
(1) Enis Chenchene, Department of Mathematics and Scientific Computing, University of Graz;
(2) Hui Huang, Department of Mathematics and Scientific Computing, University of Graz;
(3) Jinniao Qiu, Department of Mathematics and Statistics, University of Calgary.
Table of Links
2.1 Quantitative Laplace principle
2.2 Global convergence in mean-field law
3 Numerical experiments and 3.1 One-dimensional illustrative example
3.2 Nonlinear oligopoly games with several goods
4 Conclusion, Acknowledgments, Appendix, and References
3.2 Nonlinear oligopoly games with several goods

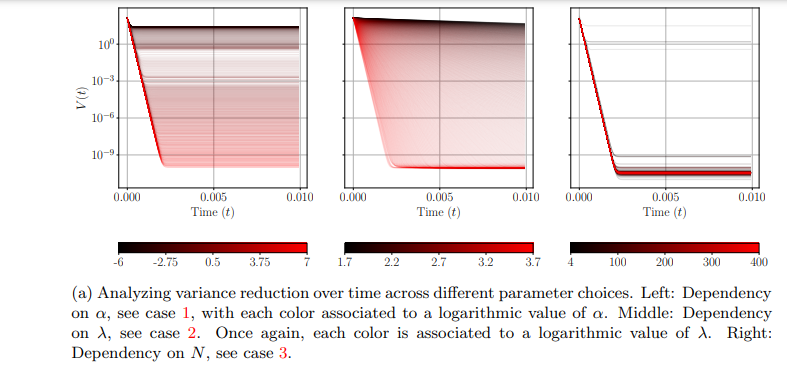
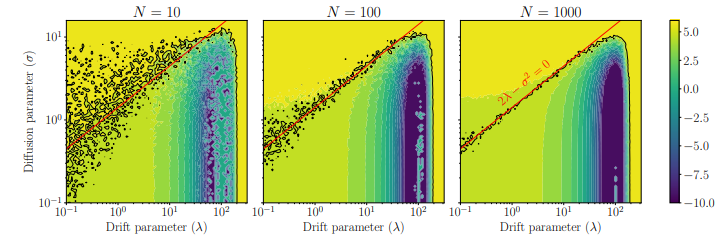
Figure 2: Studying the dependence of Algorithm 1 with respect to the algorithm’s parameters to solve (3.5).
of good produced, namely

3.2.1 Experimental setup

3.2.2 Results and discussio
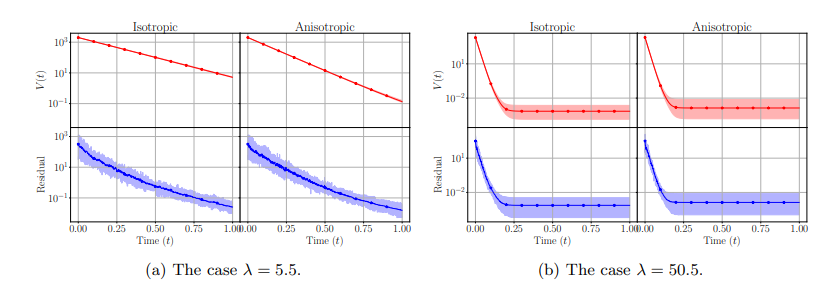
In Figure 3, which shows the results corresponding to the experiment in case 1, as observed for instance in [28], we see that the anisotropic case does indeed show a faster convergence rate especially in the initial iterations and for λ which is of the order of σ 2 . If λ increases, though, we see no significant differences in the convergence behavior of anisotropic or isotropic dynamics, both for the residual and for the variance decrease.
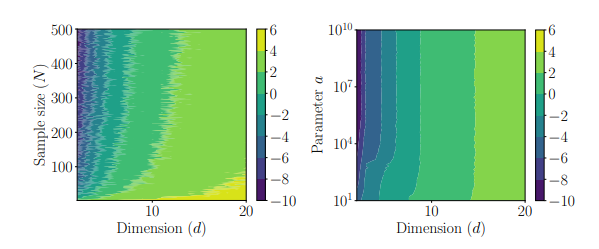
Figure 4 shows the results of the comparisons in cases 3 and 2. Regarding case 2, we can see that indeed as the dimension increases, we need exponentially many particles (quantified by N) to reach high accuracy of order 10−9 . This indicates that Algorithm 1, while being quite reliable, and sometimes the only available solver for low-dimensional problems, might need further improvement in high-dimensional settings.

This paper is available on arxiv under CC BY 4.0 DEED license.

