Scientific American, Volume XXIV., No. 12, March 18, 1871 by Various, is part of the HackerNoon Books Series. You can jump to any chapter in this book here. Answer to Practical Problem.
Answer to Practical Problem.
Messrs. Editors;—I submit the following solution of "Practical Problem" on page 147:
Given AB, arm, C, arm, D, chord of half angle of oscillation of arm, D, and angles of arms, with line AB.
To find angles, BAc', ABb, and length of link, E.
-
As the length of arm, D, is to the chord of arc, ab, divided by 2, so is the radius to the sine angle oscillation of arm, D, divided by 4.
-
360° is to the whole circumference as the angle bBa is to the length of arc ab.
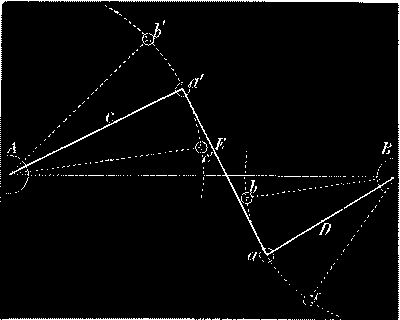
3. Now arc ab is equal to arc a'c'.
-
The whole circumference is to 360° as the length of arc a'e' is to the angle oscillation of C divided by 2.
-
Half angle oscillation, C, taken from angle BAa' is equal to angle BAc'.
-
Half angle oscillation, D, taken from angle ABa is equal to angle ABb.
-
The diagonal of the rectangle formed by the (sum of the sines of the angles of the arms with AB) into (AB—sum of cosines of same) will be the length of link, E.
G. R. Nash, Civil Engineer.
North Adams, Mass.
[We have received other solutions of this problem, but as this covers the ground in a very simple manner, we think it will be sufficient. Those forwarding the solutions not published will accept our thanks and assurances that it is not because they lack merit that they are declined.—Eds.
About HackerNoon Book Series: We bring you the most important technical, scientific, and insightful public domain books.
This book is part of the public domain. Various (2006). Scientific American, Volume XXIV., No. 12, March 18, 1871. Urbana, Illinois: Project Gutenberg. Retrieved https://www.gutenberg.org/cache/epub/19180/pg19180-images.html
This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org, located at https://www.gutenberg.org/policy/license.html.