Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
8. Evaluation of Ξ11
We first prove a general result as follows.
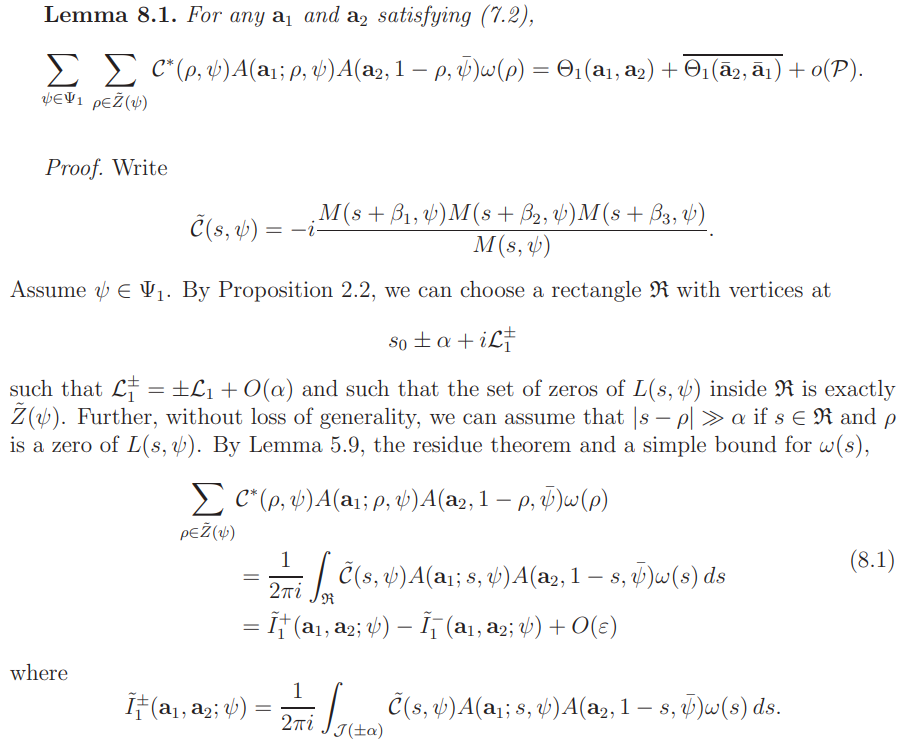

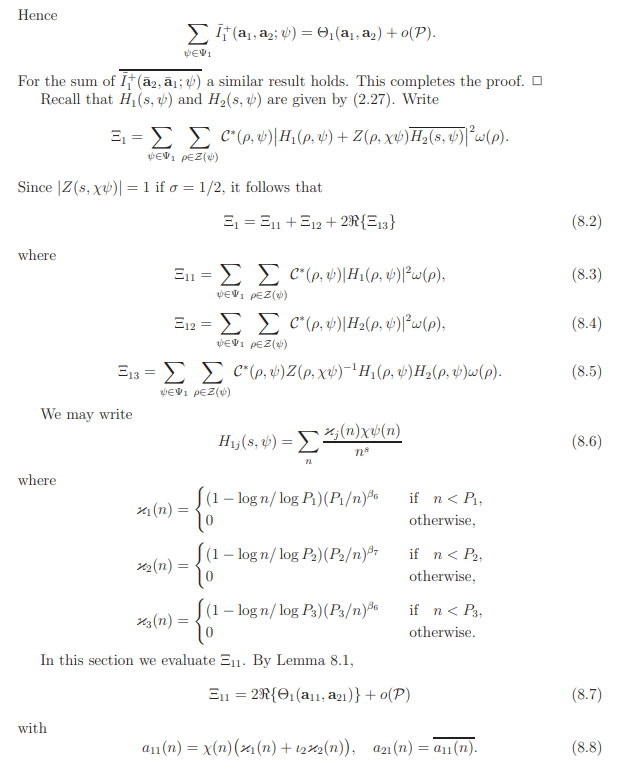
By Proposition 7.1, our goal is reduced to evaluating the sum
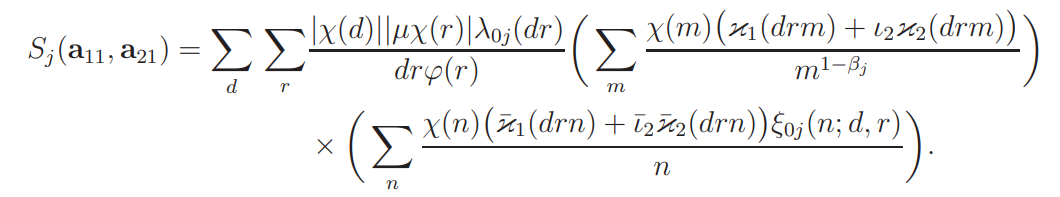
Write
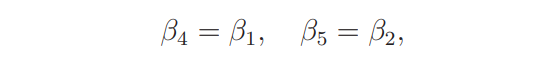
so that
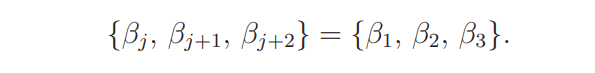
Lemma 8.2. Suppose T < x < P. Then for µ = 6, 7
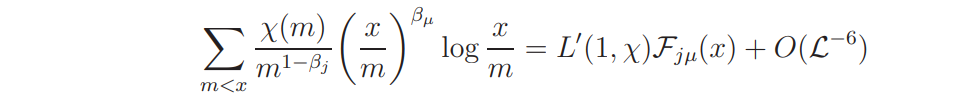
where
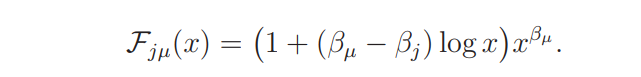
Proof. The sum is equal to
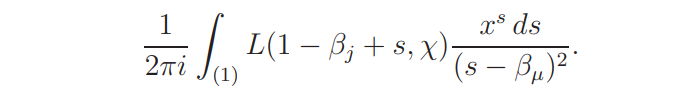
We move the contour of integration to the vertical segments
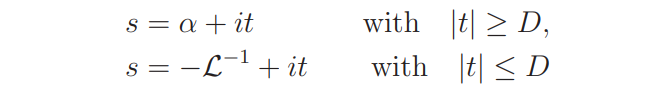
and to the two connecting horizontal segments
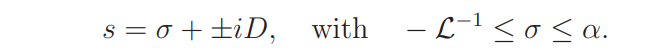
It follows by Lemma 5.6 that
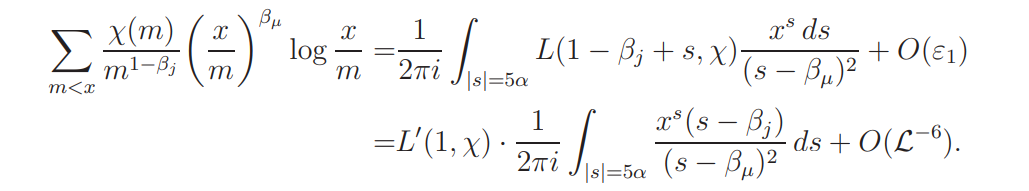
The result now follows by direct calculation.

Combining these results with Lemma 8.3, we find that the integral (8.9) is equal to
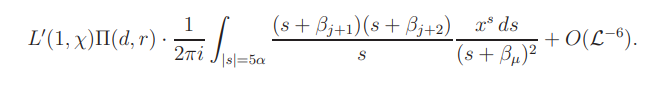
The result now follows by direct calculation.




This paper is available on arxiv under CC 4.0 license.