Scientific American Supplement, No. 711, August 17, 1889, by Various, is part of the HackerNoon Books Series. You can jump to any chapter in this book here. MAGNETISM IN ITS RELATION TO INDUCED ELECTROMOTIVE FORCE AND CURRENT.
MAGNETISM IN ITS RELATION TO INDUCED ELECTROMOTIVE FORCE AND CURRENT.
By Elihu Thomson.
There is perhaps no subject which at the present time can have a greater interest to the physicist, the electrician, and the electrical engineer than the one which heads this paper. The advances which have been made in the study from its purely theoretical or scientific side, and the great technical progress in the utilization of the known facts and principles concerning magnetic inductions, can but deepen and strengthen that interest.
On the side of pure theory we find the eager collection of experimental data to be submitted to the scrutiny of the ablest and brightest minds, to be examined and reasoned upon with the hope of finding some clew to satisfying explanations, and on the side of practice we find the search for new facts and relations no less diligent, though often stimulated by practical problems presented for solution. Indeed, the urgency for results is often the greater on the practical side, for theory can wait, practice cannot, at least in the United States.
We must look for continued triumphs in both directions, and the most welcome of all will be the framing of a theory or explanation which will enable us to interpret magnetic and electric phenomena. The recent beautiful experiments of Hertz on magnetic waves have opened a fertile region for investigation.
It would seem that the study of magnetism and electricity will give us the ability to investigate the ether of space, which medium has been theorized upon at great length, with the result of leaving it very much where it was before, a mysterious necessity.
Faraday says, speaking of magnetism:
"Such an action may be a function of the ether, for it is not at all unlikely that if there be an ether it should have other uses than simply the conveyance of radiations." 3,075. Vol. III., Exp. Res.
"It may be a vibration of the hypothetical ether, or a state of tension of that ether equivalent to either a dynamic or a static condition," etc. 3,263. Vol. III., Exp. Res.
Faraday again says, speaking of the magnetic power of a vacuum:
"What that surrounding magnetic medium deprived of all material substance may be I cannot tell, perhaps the ether." 3,277. Vol. III., Exp. Res.
Modern views would seem to point that through a study of magnetic phenomena we may take a feeble hold upon the universal ether. Magnetism is an action or condition of that medium, and it may be that electrical actions are the expression of molecular disturbances brought about by ether strains or interferences. The close relations which are shown to exist between magnetism and light tend to strengthen such views. Indeed, it would not be too much to expect that if the mechanics of the ether are ever worked out, we should find the relation between sensible heat and electric currents to be as close as that of light to magnetism, perhaps find ultimately the forms of matter, the elements and compounds to be the more complex manifestations of the universal medium—aggregations in stable equilibrium. It is a difficult conception, I confess, and a most shadowy and imperfect one, yet facts and inferences which favor such views are not wanting.
Our science of electricity seems almost to be in the same condition that chemistry was before the work of Lavoisier had shed its light on chemical theory. Our store of facts is daily increasing, and apparently disconnected phenomena are being brought into harmonious relation. Perhaps the edifice of complete theory will not be more than begun in our time, perhaps the building process will be a very gradual one, but I cannot refrain from the conviction that the intelligence of man will, if it has time, continue its advance until such a structure exists.
I have been led to make these general allusions to electrical theory in order to emphasize the fact that in the present paper no unraveling of the mystery is to be attempted, but rather the presentation of some few considerations upon a subject of absorbing interest.
The conception of Faraday in regard to the existence of lines of magnetic force representing directions of magnetic strain or tension in a medium has not only lost nothing of its usefulness up to the present time, but has continually been of great service in the understanding of magnetic phenomena. We need spend no time in showing, as Faraday and others have done, that these lines are always closed circuits, polarized so that the direction of the lines cannot be reversed without reversal of the actions. Nor need we take time to show that in any medium the lines are mutually repellent laterally if of the same direction of polarization. Opposing this tendency to separation or lateral diffusion of magnetic force is the strong apparent tendency of the lines to shorten themselves in any medium. These actions are distributed by the presentation of a better medium, as iron instead of space or air. Lines of force will move into the better medium, having apparently the constant tendency to diminish the resistance in their paths.
The peculiar and mysterious nature of media, such as iron, is to permit an extraordinary crowding of lines on account of slight resistance to their passage through it. We need not, in addition, do more than refer to the other well-known facts of an electric current developing magnetic lines encircling the conductor, as being the general type, which includes all forms of magnetic field or electro-magnets, sustained by currents, and the fact of a development when magnetic lines or circuits and material masses are in relative movement of electromotive forces transversely to the direction of the lines of magnetism, and also transversely to the direction of relative movement, as in the case of electric conductors traversing or cutting through a field, or of a field traversing or being moved across a conductor. We must not forget that even insulators, as well as conductors, cutting lines of force, have the electromotive force developed in them. The action simply develops potential difference, and this generates the current where a circuit exists. While we are in the habit of saying that a conductor moved across a field of lines, or vice versa, generates electric current, I think the statement incomplete. The movement only sets up a potential difference, and the power expended in effecting the movement generates C × E. The current is energy less the potential, or the energy expended gives the two effects of potential or pressure and current or rate of movement. Consequently an insulator, or an open-circuited conductor, traversing a field, consumes no energy, potential difference only being produced. Nevertheless, as will be shown, the magnetic circuits or lines themselves may furnish the energy for their own movement across a conductor, and so develop current as well as potential.
This occurs in the effort of lines to shorten their paths, to lessen their density, to pass to better media. Indeed, a close examination will show that wherever power is expended in developing current in a circuit, cutting lines of force, the energy expended is first employed in stretching the lines, which thus receive the energy required to permit them, in shortening, to cut the conductor and set up currents in the electric circuit in accordance with the potential difference developed in that circuit and its resistance.
I think we may also say, though I do not remember to have seen the statement so put, that whenever electric potential is set up inductively, as in self-induction, mutual induction, induction from one circuit to another, and induction from magnets or magnetic field, it is set up by the movement of lines of force laterally across the body, mass or conductor in which the potential is developed, and that whenever current is set up in a wire or an existing current prolonged, or an existing current checked by induction, self-induction, or induction from magnets, the action is a transfer of energy, represented by strained lines of force shortening or lessening their resistance, or lengthening and increasing the resistance in their paths. The magnetic field is like an elastic spring—it can in one condition represent stored energy—it can be strained and will store energy—it can be made to relieve its strain and impart energy.
Let us examine some known phenomena in this light. Take the case of a simple wire, conveying current, say, in a line away from observer, Fig. 1. There exists a free field of circular magnetism (so called), shading off away from the wire, and which is represented by concentric circles of increased diameter. The superior intensity or strength of the lines near the wire may also be represented by their thickness. This is often shown also by crowding the lines near the wire, though I am disposed to regard Fig. 1 as more nearly expressing the condition, unless we are to regard the lines as simply indicating a sort of atmosphere of magnetic effect whose density becomes less as we proceed outward from the wire, in which case either form of symbol suffices. The direction of polarization of the lines may be indicated by an arrow head pointing in a direction of right-handed rotation in the path of the lines. This is the typical figure or expression for all forms of simple magnetic circuit—the form of the lines, their length, position, density, will depend on the shape of the conductor or conductors (when more than one) and the materials surrounding or in proximity to the wire or wires.
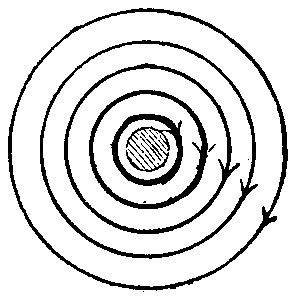
If the current traversing the conductor is constant, the magnetic field around it is stable and static, unless other influences come in to modify it. The cutting off of the current is followed by instability of the field whereby it can and must produce dynamic effects. I say must because the field represents stored energy, and in disappearing must give out that energy. To throw light on this part of the subject is one of the objects of the present paper. Cutting off the current supply in the case assumed leaves the developed magnetic lines or strains unsupported. They at once shorten their paths or circuits, collapsing upon the conductor as it were, and continuing this action, cut the section of the conductor, and apparently disappear in magnetic closed circuits of infinitesimal diameter but of great strength of polarization. It appears to me that we must either be prepared to give up the idea of lines of force or take the position that the magnetic circuits precipitate themselves in shortening their circuits and disappearing upon and cut the conductor. It was Hughes who put forward the idea that an iron bar in losing its apparent magnetism really short-circuits the lines in itself as innumerable strongly magnetized closed circuits among the molecules. In becoming magnetic once more these short circuits are opened or extended into the air by some source of energy applied to strain the lines, such as a current in a conductor around the bar.
May not this idea be extended, then, to include the magnetic medium, the ether itself? Does it contain intensely polarized closed circuits of magnetism which are ready to be stretched or extended under certain conditions by the application of energy, which energy is returned by the collapse of the extended circuits? This is doubtless but a crude expression of the real condition of things, for the lines are only symbols for a condition of strain in a medium which cannot be represented in thought, as we know nothing of its real nature. There is one point in this connection which I must emphasize. The strained lines, Fig. 1, are indications of stored energy in the ether, and the lines cannot disappear without giving out that energy. Ordinarily, it makes its appearance as the extra current, and adds itself so as to prolong the current which extended the lines when an attempt is made to cut off such current. Were it conceivable that the current could be cut off and the wire put on open circuit while the lines still remained open or strained, the energy must still escape when the field disappears. It would then produce such a high potential as to be able to discharge from the ends of the conductor, and if the conductor were of some section, part of the energy would be expended in setting up local currents in it. The field could not disappear without an outlet for the energy it represents. But we cannot cut off a current in a wire so as to leave the wire on open circuit with the lines of the magnetic circuit remaining around it without iron or steel or the like in the magnetic circuit. We can approach that condition, however, by breaking the circuit very quickly with a condenser of limited capacity around the break. This is done in the Ruhmkorff coil primary; the condenser forms a sort of blind alley for the extra current on its beginning to flow out of the primary coil. But the condenser charges and backs up and stops the discharge from the primary, even giving a reverse current. The lines of magnetic force collapse, however, and have their effect in the enormous potential set up in the secondary coil.
Take away the secondary coil so as to stop that outlet, the energy expends itself on the iron core and the primary coil. Take away the iron core, and the energy of magnetization of the air or ether core expends itself on the wire of the primary and, possibly, also on the dielectric of the condenser to some extent. The extra current becomes in this instance an oscillatory discharge of very high period back and forth through the primary coil from the condenser, until the energy is lost in the heat of C2 × R. This conversion is doubtless rendered all the more rapid by uneven distribution of current and eddy current set up in the wire of the coil.
The considerations just given concern the loss of field or the shortening and apparent disappearance of the magnetic lines or circuits, as giving rise to the self-induction or increased potential on breaking. Where the energizing current is slowly cut off or diminished the energy is gradually transferred to the wire in producing elevation of potential during the decrease; and the collapse and cutting of the wire by the collapsing circuits or lines is then only more gradual.
Let the current be returned to the wire after disappearance of magnetism, and the lines again seem to emanate from the wire and at the same time cut it and produce a counter potential in it, which is the index of the abstraction of energy from the circuit, and its storing up in the form of elastically strained lines of magnetism around the conductor. The effect is that of self-induction on making or upon increase of current, the measure of the amount being the energy stored in the magnetic circuits which have been extended or opened up by the current. The greater the current and the shorter the path for the lines developed around the axis of the conductor, the greater the energy stored up. Hence, a circular section conductor has the highest self-induction, a tube of same section less as its diameter increases, a flat strip has less as its width increases and thickness diminishes, a divided conductor much less than a single conductor of same shape and section. Separating the strands of a divided conductor increases the length of magnetic paths around it, and so diminishes the self-induction. A striking instance of this latter fact was developed in conveying very heavy alternating currents of a very low potential a distance of about three feet by copper conductors, the current being used in electric welding operations.
The conductors were built up of flat thin strips of copper for flexibility. When the strips were allowed to lie closely together, the short conductor showed an enormous self-induction, which cut down the effective potential at its ends near the work. By spreading apart the strips so as to lengthen a line around the conductor, the self-induction could be easily made less than 35 per cent. of what it had been before. The interweaving of the outgoing and return conductor strands as one compound conductor gets rid almost entirely of the self-inductive effects, because neither conductor has any free space in which to develop strong magnetic forces, but is opposed in effect everywhere by the opposite current in its neighbor.
Where a number of conductors are parallel, and have the same direction of current, as in a coil or in a strand, it is evident that statically the conductor may be considered as replaceable by a single conductor with the same external dimensions and same total current in the area occupied, the magnetic forces or lines surrounding them being of same intensity. But with changing current strength the distribution of current in the conductor has also a powerful effect on the energy absorbed or given out in accordance with the magnetism produced. Hence the self-induction of a strand, coil or conductor of the same section varies with the rapidity of current changes, owing to the conduction being uneven.
The uneven distribution of current, or its tendency to flow on the outer parts of a conductor when the rate of variation or alternation is made great, is in itself a consequence of the fact that less energy is transferred into magnetism in this case than when the current flows uniformly over the section, or is concentrated at the center. In other words, when a uniform current traverses a conductor of the same section, the circular magnetism, or surrounding magnetic lines, are to be found not only outside the conductor, but also beneath its exterior. Since in forming these lines on passage of current the middle of section would be surrounded by more lines than any other part of the conductor, the current tends to keep out of that part and move nearer the exterior in greater amount. Hence, in rapidly alternating currents the conductor section is practically lessened, being restricted largely to the outer metal of the conductor. If the round conductor, Fig. 2, were made of iron, the magnetism interior to it and set up by a current in it would be very much greater, the section of the conductor being filled with magnetic circuits or lines around the center. The total magnetism, external and internal, would be much greater in this case for a given current flow, and the energy absorbed and given out in formation and loss of field or the self-induction would be much increased. This could, however, be greatly diminished by slitting the conductor radially or making it of a number of separate wires out of lateral magnetic contact one with the other, Fig. 3. In these cases the resistance of the interior magnetic circuits would be increased, as there would be several breaks in the continuity around the center of the conductor. The total magnetism which could be set up by a current would be lessened, and the self-induction, therefore, lessened.
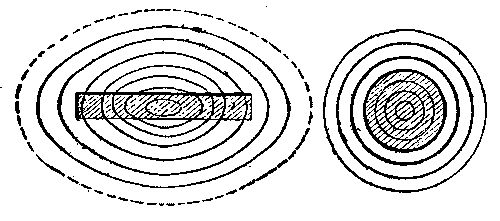

The moment we begin the bringing of iron into proximity with an electric conductor conveying current, we provide a better medium for the flow or development of magnetic lines or circuits. In other words, the lines may then be longer, yet equally intense, or more lines may be crowded into a section of this metal than in air or space. Figs. 4a, 4b, 4c show the effect brought about by bringing iron of different forms near to the conductor.
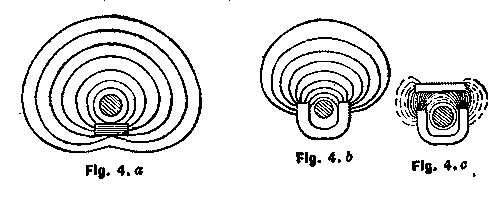
It shows, in other words, the development of the ordinary electro-magnet of the horseshoe form, and the concentration of the lines in the better medium. The lines also tend to shorten and diminish the resistance to their passage, so that attraction of the iron to the conductor takes place, and if there is more than one piece of iron, they tend to string themselves around the conductor in magnetic contact with one another.
When copper bars of 1 inch diameter are traversed by currents of 40,000 to 60,000 amperes, as in welding them, the magnetic forces just referred to become so enormous that very heavy masses of iron brought up to the bar are firmly held, even though the current be of an alternating character, changing direction many times a second.
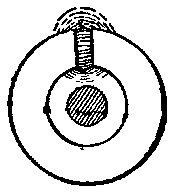
When a conductor is surrounded by a cast iron ring, as in Fig. 5, the current in such conductor has an excellent magnetic medium surrounding it. A large amount of energy is then abstracted on the first impulse of current, which goes to develop strong and dense magnetic lines through the iron ring and across the gap in it. On taking off the current the energy is returned as extra current, and its force is many times what would be found with air alone surrounding the conductor. We have then greatly increased the self-induction, the storing of energy and opposition to current flow at the beginning, the giving back of energy and assistance to the current flow on attempting to remove or stop the current. Let us now complete the ring, by making it of iron, endless, Fig. 6, with the conductor in the middle.
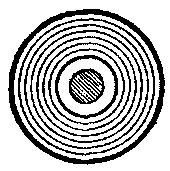
We now find that on passing current through the conductor it meets with a very strong opposing effect or counter potential. The evolution of magnetic lines, or the opening out of magnetic circuits, goes on at a very rapid rate. Each line or magnetic circuit evolved, and cutting the conductor, flies at once outward, and locates itself in the iron ring. This ring can carry innumerable lines, and they do not crowd one another. It permits the lines even to lengthen in reaching it, and yet, on account of its low resistance to their passage, the lengthening is equivalent to their having shortened in other media. We will suppose the current not sufficient to exhaust this peculiar capacity for lines which the iron has. Equilibrium is reached, the conductor has opened up innumerable closed circuits, and caused them to exist in the ring still closed; but in iron, not space or ether merely. The current passing has continued its action and storage of energy until to emit another line in view of the resistance now found in the crowded iron ring is impossible.
Now let us cut off the current. We are surprised to find a very weak extra current, a practical absence of self-induction on breaking, or, at least, a giving out of energy in nowise comparable to that on making. Let us put on the current as it was before. Another curious result. But little self-induction now on making energy not absorbed.
Now cut off the current again. Same effect as before. Now let us put on the current reversed in direction. At once we find a very strong counter potential or opposing self-induction developed.
The ring had been polarized, or retained its magnetic energy, and we are now taking out one set of lines and putting in reversely polarized lines of force. This done, we break the reversed current without much effect of self-induction. The ring remains polarized and inert until an opposite flow of current be sent through. Iron is then a different medium from the ether.
The ring once magnetized must, in losing its magnetism, permit a closure of the lines by shortening. This involves their passage from the iron across the space in the center of the ring, notwithstanding its great resistance to the lines of force. As passage from iron to air is equivalent to lengthening of the lines, it is readily seen that such lengthening may oppose more effect than a slight shortening due to leaving iron, for air or space may give in provoking a closure and disappearance of the lines. Looked at from another standpoint, the lines on the iron may actually require a small amount of initial energy to dislodge them therefrom, so that after being dislodged they may collapse and yield whatever energy they represent.
I must reserve for the future further consideration of the iron ring, but in thinking upon this matter I am led to think that the production of a magnetic line in an iron ring around a conductor may represent a sort of wave of energy, an absorption of energy on the evolution of the line from the conductor, and a slight giving out of energy on the line reaching that position of proximity to the iron ring, that its passage thereto may be said to be a shortening process or a lessening of its resistance.
The magnetism in air, gases, and non-magnetic bodies, being assumed to be that of the ether, this medium shows no such effects as those we get with the ring. It does not become permanently polarized, as does even soft iron under the condition of a closed ring. The iron possesses coercive force, or magnetic rigidity, and a steel ring would show more of it. The molecules of the iron or steel take a set. If we were to cut the soft iron ring, or separate it in any way, this introduction of resistance of air for ether in the magnetic circuit would cause the lines to collapse and set up a current in the conductor. The energy of the ring would have been restored to the latter. The curious thing is that physically the polarized ring does not present any different appearance or ordinary properties different from those of a plain ring, and will not deflect a compass needle. Its condition is discoverable, however, by the test of self-induction to currents of different direction. As a practical consideration, we may mention in this connection that a self-inductive coil for currents of one direction must be constructed differently from one to be used with alternating currents. The former must have in its magnetic circuit a section of air or the like, or be an imperfectly closed circuit, as it were. The latter should have as perfectly closed a magnetic circuit as can be made. We see here also the futility of constructing a Ruhmkorff core coil on the closed iron magnetic circuit plan, because the currents in the primary are interrupted, not reversed.
The considerations just put forward in relation to the closed iron ring, and its passive character under the condition of becoming polarized, are more important than at first appears. It has been found that the secondary current wave of a closed iron circuit induction coil or transformer, whose primary circuit receives alternating current, is lagged from its theoretical position of 90 degrees behind the primary wave an additional 90 degrees, so that the phases of the two currents are directly opposed; or the secondary current working lamps only in its circuit is one half a wave length behind a primary, instead of a quarter wave length, as might have been expected.
But when it is understood that the iron core polarized in one direction by the primary impulse does not begin to lose its magnetism when that impulse simply weakens, but waits until an actual reversal of current has taken place, it will be seen that the secondary current, which can only be produced when magnetic lines are leaving the core and cutting the secondary coil, or when the lines are being evolved and passing into the core from the primary coil, will have a beginning at the moment the primary reverses, will continue during the flow of that impulse, and will end at substantially the same time with the primary impulse, provided the work of the secondary current is not expended in overcoming self-induction, which would introduce a further lag. Moreover, the direction of the secondary current will be opposite to that of the primary, because the magnetic circuits which are opened up by the primary current in magnetizing the core, or which are closed or collapsed by it in demagnetizing the core, will always cut the secondary coil in the direction proper for this result. Transformers of the straight core type with very soft iron in the cores and not too high rates of alternation should approximate more nearly the theoretical relation of primary and secondary waves, because the magnetic changes in the core are capable of taking place almost simultaneously with the changes of strength of the primary current. This fact also has other important practical and theoretical bearings.
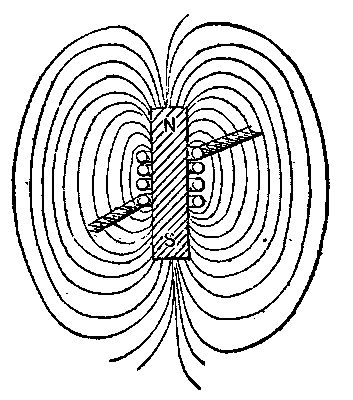
Let us assume a plain iron core, Fig. 7, magnetized as indicated, so that its poles, N, S, complete their magnetic circuits by what is called free field or lines in space around it. Let a coil of wire be wound thereon as indicated. Now assume that the magnetism is to be lost or cease, either suddenly or slowly. An electric potential will be set up in the coil, and if it has a circuit, work or energy will be produced or given out in that circuit, and in any other inductively related to it. Hence the magnetic field represents work or potential energy. But to develop potential in the wire the lines must cut the wire. This they can do by collapsing or closing on themselves. The bar seems, therefore, to lose its magnetism by gaining it all, and in doing so all the external lines of force moving inward cut the wire. The magnetic circuits shorten and short-circuit themselves in the bar, perhaps as innumerable molecular magnetic circuits interior to the iron medium. To remagnetize the bar we may pass an electric current through the coil. The small closed circuits are again distended, the free field appears, and the lines moving outward cut across the wire coil opposite to the former direction and produce a counter potential in the wire, and consequent absorption of the energy represented in the free field produced. As before studied, the magnetism cannot disappear without giving out the energy it represents, even though the wire coil be on open circuit, and therefore unable to discharge that energy. The coil open-circuited is static, not dynamic. In such assumed case the lines in closing cut the core and heat it. Let us, however, laminate the core or subdivide it as far as possible, and we appear to have cut off this escape for the energy. This is not really so, however. We have simply increased the possible rate of speed of closure, or movement of the lines, and so have increased for the divided core the intensity of the actions of magnetic friction and local currents in the core, the latter still receiving the energy of the magnetic circuit. This reasoning is based on the possibility in this case of cutting off the current in the magnetizing coil and retaining the magnetic field. This is of itself probably impossible with soft iron. That the core receives the energy when the coil cannot is shown in the well known fact that in some dynamos with armatures of bobbins on iron cores, the running of the armature coils on open circuit gives rise to dangerous heating of the cores, and that under normal work the heating is less. In the former case the core accumulates the energy represented in the magnetic changes. In the latter the external circuit of the machine and its wire coils take the larger part of the energy which is expended in doing the work in the circuit. In this case, also, the current in the coils causes a retardation of the speed of change and extent of change of magnetism in the iron cores, which keeps down the intensity of the magnetic reaction. In fact, this retardation or lag and reduction of range of magnetic change may in some machines be made so great by closing the circuit of the armature coils themselves or short-circuiting them that the total heat developed in the cores is much less than under normal load.
I wish now, in closing, to refer briefly to phenomena of moving lines of force, and to the effects of speed of movement. In order to generate a given potential in a length of conductor we have choice of certain conditions. We can vary the strength of field and we can vary the velocity. We can use a strong field and slow movement of conductor, or we can use a weak field and rapid movement of the conductor. But we find also that where the conductor has large section it is liable to heat from eddy currents caused by one part of its section being in a stronger field than another at the same time. One part cuts the lines where they are dense and the other where they are not dense, with the result of difference of potential and local currents which waste energy in heat. We cannot make the conductor move in a field of uniform density, because it must pass into and out of the field. The conditions just stated are present in dynamos for heavy current work, where the speed of cutting of lines is low and the armature conductor large in section.
But we find that in a transformer secondary we can use very large section of conductor, even (as in welding machines) 12 to 15 square inches solid copper, without meeting appreciable difficulty from eddy currents in it. The magnetic lines certainly cut the heavy conductor and generate the heavy current and potential needed. What difference, if any, exists? In the transformer the currents are generated by magnetic field of very low density, in which the lines are moving across the conductor with extreme rapidity. The velocity of emanation of lines around the primary coil is probably near that of light, and each line passes across the section secondary conductor in a practically inappreciable time. There is no cause then for differences of potential at different parts of the section heavy secondary. Then to avoid eddy currents in large conductors and generate useful currents in them, we may cause the conductor to be either moved into and out of a low density field with very great speed, or better, we must cause the lines of a very low or diffused field to traverse or cut across the conductor with very high velocity.
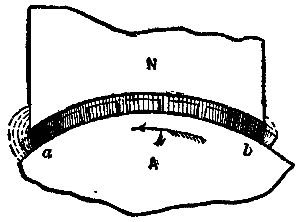
It is a known fact that, in dynamos with large section armature conductors, there are less eddy currents produced in the conductors when they are provided with iron cores or wound upon iron cores than when the conductors are made into flat bobbins moved in front of field poles. Projections existing on the armature between which the conductors are placed have a like effect, and enable us to employ heavy bars or bundles of wire without much difficulty from local currents. The reason is simple. In the armatures with coils without iron in them, or without projections extending between the turns, the conductor moves into and out of a very dense field at comparatively low velocity, so that any differences of potential developed in the parts of the section of conductor have full effect and abundant time to act in setting up harmful local currents. In the cases in which iron projects through the coil or conductor, the real action is that the lines of the magnetic circuits move at high speeds across the conductor, and the conductor is at all times in a field of very low density. Figs. 8 and 9 will make this plain. In Fig. 8 we have shown a smooth armature surface, having a heavy conductor laid thereon, and which is at a just entering a dense field at the edge of the pole, N, and at b leaving such field. It will be seen that when in such position the conductor, if wide, is subjected to varying field strength, and moves at a low speed for the generation of the working potential as it passes through the field, thus giving rise to eddy currents in the conductor.
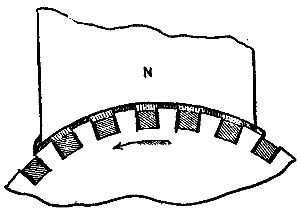
In Fig. 9 the conductors are set down between projections, in which case both armature and field poles are laminated or subdivided. As each projection leaves the edge of field pole, N, the lines which it had concentrated on and through it snap backward at an enormous speed, and cross the gap to the next succeeding projection on the armature, cutting the whole section of the heavy armature conductor at practically the same instant. This brisk transfer of lines goes on from each projection to the succeeding one in front of the field pole, leaving a very low density of field at any time between the projections. The best results would be obtained when the armature conductor does not project beyond or quite fill the depth of groove between the projections. Of course there are other remedies for the eddy current difficulty, notably the stranding and twisting of the conductor on the armatures so as to average the position of the parts of the compound conductor.
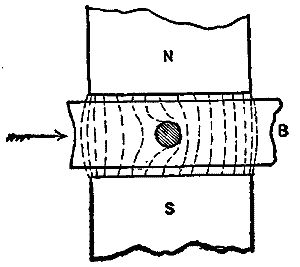
Perhaps the most extreme case of what may be called dilution of field by projections and by closed magnetic circuits in transformers would be that of a block of iron, B, Fig. 10, moved between poles, N and S, and having a hole through it, into and through which a conductor is carried. The path through the iron is so good that we can scarcely consider that any lines cross the hole from N to S; yet as B moves forward there is a continual snapping transfer of lines from the right forward side of the hole to the left or backward side, cutting the conductor as they fly across, and developing an electromotive force in it. I have described this action more in detail because we have in it whatever distinction in the manner of cutting the lines of the field is to be found between wire on smooth armatures and on projection armatures and modifications thereof; and also between flat, open coils passing through a field and bobbins with cores of iron. The considerations advanced also bring out the relation which exists between closed iron circuit transformers and closed iron circuit (projection) dynamos, as we may call them.
I had intended at the outset of this paper to deal to some extent with the propagation of lines of magnetism undergoing retardation in reference to alternating current motor devices, transformers with limited secondary current, or constant average current, an alternating motor working with what I may term a translation lag, etc.; but it was soon found that these matters must remain over for a continuation of this paper at some future time. My endeavor has been in the present paper to deal with the lines of force theory as though it were a symbol of the reality, but I confess that it is done with many misgivings that I may have carried it too far. Yet, if we are to use the idea at all it has seemed but right to apply it wherever it may throw any light on the subject or assist in our understanding of phenomena.
A paper read before the American Institute of Electrical Engineers, New York, May 22, 1889.
About HackerNoon Book Series: We bring you the most important technical, scientific, and insightful public domain books.
This book is part of the public domain. Various (2004). Scientific American Supplement, No. 711, August 17, 1889. Urbana, Illinois: Project Gutenberg. Retrieved https://www.gutenberg.org/cache/epub/16972/pg16972-images.html
This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org, located at https://www.gutenberg.org/policy/license.html.

