Scientific American Supplement, No. 717, September 28, 1889, by Various, is part of the HackerNoon Books Series. You can jump to any chapter in this book here. QUARTZ FIBERS.
QUARTZ FIBERS.
In almost all investigations which the physicist carries out in the laboratory, he has to deal with and to measure with accuracy those subtile and to our senses inappreciable forces to which the so-called laws of nature give rise. Whether he is observing by an electrometer the behavior of electricity at rest or by a galvanometer the action of electricity in motion, whether in the tube of Crookes he is investigating the power of radiant matter, or with the famous experiment of Cavendish he is finding the mass of the earth—in these and in a host of other cases he is bound to measure with certainty and accuracy forces so small that in no ordinary way could their existence be detected, while disturbing causes which might seem to be of no particular consequence must be eliminated if his experiments are to have any value. It is not too much to say that the very existence of the physicist depends upon the power which he possesses of producing at will and by artificial means forces against which he balances those that he wishes to measure.
I had better perhaps at once indicate in a general way the magnitude of the forces with which we have to deal.
The weight of a single grain is not to our senses appreciable, while the weight of a ton is sufficient to crush the life out of any one in a moment. A ton is about 15,000,000 grains. It is quite possible to measure with unfailing accuracy forces which bear the same relation to the weight of a grain that a grain bears to a ton.
To show how the torsion of wires or threads is made use of in measuring forces, I have arranged what I can hardly dignify by the name of an experiment. It is simply a straw hung horizontally by a piece of wire. Resting on the straw is a fragment of sheet iron weighing ten grains. A magnet so weak that it cannot lift the iron yet is able to pull the straw round through an angle so great that the existence of the feeble attraction is evident to every one in the room.
Now it is clear that if, instead of a straw moving over the table simply, we had here an arm in a glass case and a mirror to read the motion of the arm, it would be easy to observe a movement a hundred or a thousand times less than that just produced, and therefore to measure a force a hundred or a thousand times less than that exerted by this feeble magnet.
Again, if instead of wire as thick as an ordinary pin I had used the finest wire that can be obtained, it would have opposed the movement of the straw with a far less force. It is possible to obtain wire ten times finer than this stubborn material, but wire ten times finer is much more than ten times more easily twisted. It is ten thousand times more easily twisted. This is because the torsion varies as the fourth power of the diameter. So we say 10 × 10 = 100, 100 × 100 = 10,000. Therefore, with the finest wire, forces 10,000 times feebler still could be observed.
It is therefore evident how great is the advantage of reducing the size of a torsion wire. Even if it is only halved, the torsion is reduced sixteenfold. To give a better idea of the actual sizes of such wires and fibers as are in use, I shall show upon the screen a series of such photographs taken by Mr. Chapman, on each of which a scale of thousandths of an inch has been printed.




The first photograph (Fig. 1) is an ordinary hair—a sufficiently familiar object, and one that is generally spoken of as if it were rather fine. Much finer than this is the specimen of copper wire now on the screen (Fig. 2), which I recently obtained from Messrs. Nalder Brothers. It is only a little over one-thousandth of an inch in diameter. Ordinary spun glass, a most beautiful material, is about one-thousandth of an inch in diameter, and this would appear to be an ideal torsion thread (Fig. 3). Owing to its fineness, its torsion would be extremely small, and the more so because glass is more easily deformed than metals. Owing to its very great strength, it can carry heavier loads than would be expected of it. I imagine many physicists must have turned to this material in their endeavor to find a really delicate torsion thread. I have so turned only to be disappointed. It has every good quality but one, and that is its imperfect elasticity. For instance, a mirror hung by a piece of spun glass is casting an image of a spot of light on the scale. If I turn the mirror, by means of a fork, twice to the right, and then turn it back again, the light does not come back to its old point of rest, but oscillates about a point on one side, which, however, is slowly changing, so that it is impossible to say what the point of rest really is. Further, if the glass is twisted one way first and then the other way, the point of rest moves in a manner which shows that it is not influenced by the last deflection alone: the glass remembers what was done to it previously. For this reason spun glass is quite unsuitable as a torsion thread; it is impossible to say what the twist is at any time, and therefore what is the force developed.

So great has the difficulty been in finding a fine torsion thread that the attempt has been given up, and in all the most exact instruments silk has been used. The natural cocoon fibers, as shown on the screen (Fig. 4), consist of two irregular lines gummed together, each about one two-thousandth of an inch in diameter. These fibers must be separated from one another and washed. Then each component will, according to the experiment of Gray, carry nearly 60 grains before breaking, and can be safely loaded with 15 grains. Silk is therefore very strong, carrying at the rate of from 10 to 20 tons to the square inch. It is further valuable in that its torsion is far less than that of a fiber of the same size of metal or even of glass, if such could be produced. The torsion of silk, though exceedingly small, is quite sufficient to upset the working of any delicate instrument, because it is never constant. At one time the fiber twists one way and another time in another, and the evil effect can only be mitigated by using large apparatus in which strong forces are developed. Any attempt that may be made to increase the delicacy of apparatus by reducing their dimensions is at once prevented by the relatively great importance of the vagaries of the silk suspension.
The result, then, is this. The smallness, the length of period, and therefore delicacy, of the instruments at the physicist's disposal have until lately been simply limited by the behavior of silk. A more perfect suspension means still more perfect instruments, and therefore advance in knowledge.
It was in this way that some improvements that I was making in an instrument for measuring radiant heat came to a deadlock about two years ago. I would not use silk, and I could not find anything else that would do. Spun glass, even, was far too coarse for my purpose, it was a thousand times too stiff.

There is a material invented by Wollaston long ago, which, however, I did not try because it is so easily broken. It is platinum wire which has been drawn in silver, and finally separated by the action of nitric acid. A specimen about the size of a single line of silk is now on the screen, showing the silver coating at one end (Fig. 5).
As nothing that I knew of could be obtained that would be of use to me, I was driven to the necessity of trying by experiment to find some new material. The result of these experiments was the development of a process of almost ridiculous simplicity which it may be of interest for me to show.
The apparatus consists of a small crossbow, and an arrow made of straw with a needle point. To the tail of the arrow is attached a fine rod of quartz which has been melted and drawn out in the oxyhydrogen jet. I have a piece of the same material in my hand, and now after melting their ends and joining them together, an operation which produces a beautiful and dazzling light, all I have to do is to liberate the string of the bow by pulling the trigger with one foot, and then if all is well a fiber will have been drawn by the arrow, the existence of which can be made evident by fastening to it a piece of stamp paper.
In this way threads can be produced of great length, of almost any degree of fineness, of extraordinary uniformity, and of enormous strength. I do not believe, if any experimentalist had been promised by a good fairy that he might have anything he desired, that he would have ventured to ask for any one thing with so many valuable properties as these fibers possess. I hope in the course of this evening to show that I am not exaggerating their merits.


In the first place, let me say something about the degree of fineness to which they can be drawn. There is now projected upon the screen a quartz fiber one five-thousandth of an inch in diameter (Fig. 6). This is one which I had in constant use in an instrument loaded with about 30 grains. It has a section only one-sixth of that of a single line of silk, and it is just as strong. Not being organic, it is in no way affected by changes of moisture and temperature, and so it is free from the vagaries of silk which give so much trouble. The piece used in the instrument was about 16 inches long. Had it been necessary to employ spun glass, which hitherto was the finest torsion material, then, instead of 16 inches, I should have required a piece 1,000 feet long, and an instrument as high as the Eiffel tower to put it in.
There is no difficulty in obtaining pieces as fine as this yards long if required, or in spinning it very much finer. There is upon the screen a single line made by the small garden spider, and the size of this is perfectly evident (Fig. 7). You now see a quartz fiber far finer than this, or, rather, you see a diffraction phenomenon, for no true image is formed at all; but even this is a conspicuous object in comparison with the tapering ends, which it is absolutely impossible to trace in a microscope. The next two photographs, taken by Mr. Nelson, whose skill and resources are so famous, represent the extreme end of a tail of quartz, and, though the scale is a great deal larger than that used in the other photographs, the end will be visible only to a few. Mr. Nelson has photographed here what it is absolutely impossible to see. What the size of these ends may be, I have no means of telling. Dr. Royston Piggott has estimated some of them at less than one-millionth of an inch, but, whatever they are, they supply for the first time objects of extreme smallness the form of which is certainly known, and, therefore, I cannot help looking upon them as more satisfactory tests for the microscope than diatoms and other things of the real shape of which we know nothing whatever.
Since figures as large as a million cannot be realized properly, it may be worth while to give an illustration of what is meant by a fiber one-millionth of an inch in diameter.
A piece of quartz an inch long and an inch in diameter would, if drawn out to this degree of fineness, be sufficient to go all the way round the world 658 times; or a grain of sand just visible—that is, one-hundredth of an inch long and one hundredth of an inch in diameter—would make one thousand miles of such thread. Further, the pressure inside such a thread due to a surface tension equal to that of water would be 60 atmospheres.
Going back to such threads as can be used in instruments, I have made use of fibers one ten-thousandth of an inch in diameter, and in these the torsion is 10,000 times less than that of spun glass.
As these fibers are made finer their strength increases in proportion to their size, and surpasses that of ordinary bar steel, reaching, to use the language of engineers, as high a figure as 80 tons to the inch. Fibers of ordinary size have a strength of 50 tons to the inch.
While it is evident that these fibers give us the means of producing an exceedingly small torsion, and one that is not affected by weather, it is not yet evident that they may not show the same fatigue that makes spun glass useless. I have, therefore, a duplicate apparatus with a quartz fiber, and you will see that the spot of light comes back to its true place on the screen after the mirror has been twisted round twice.
I shall now for a moment draw your attention to that peculiar property of melted quartz that makes threads such as I have been describing a possibility. A liquid cylinder, as Plateau has so beautifully shown, is an unstable form. It can no more exist than can a pencil stand on its point. It immediately breaks up into a series of spheres. This is well illustrated in that very ancient experiment of shooting threads of resin electrically. When the resin is hot, the liquid cylinders, which are projected in all directions, break up into spheres, as you see now upon the screen. As the resin cools, they begin to develop tails; and when it is cool enough, i.e., sufficiently viscous, the tails thicken and the beads become less, and at last uniform threads are the result. The series of photographs show this well.
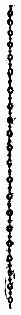
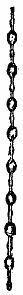
There is a far more perfect illustration which we have only to go into the garden to find. There we may see in abundance what is now upon the screen—the webs of those beautiful geometrical spiders. The radial threads are smooth like the one you saw a few minutes ago, but the threads that go round and round are beaded. The spider draws these webs slowly, and at the same time pours upon them a liquid, and still further to obtain the effect of launching a liquid cylinder in space he, or rather she, pulls it out like the string of a bow, and lets it go with a jerk. The liquid cylinder cannot exist, and the result is what you now see upon the screen (Fig. 8). A more perfect illustration of the regular breaking up of a liquid cylinder it would be impossible to find. The beads are, as Plateau showed they ought to be, alternately large and small, and their regularity is marvelous. Sometimes two still smaller beads are developed, as may be seen in the second photograph, thus completely agreeing with the results of Plateau's investigations.
I have heard it maintained that the spider goes round her web and places these beads there afterward. But since a web with about 360,000 beads is completed in an hour—that is at the rate of about 100 a second—this does not seem likely. That what I have said is true, is made more probable by the photograph of a beaded web that I have made myself by simply stroking a quartz fiber with a straw wetted with castor oil (Fig. 9); it is rather larger than a spider line; but I have made beaded threads, using a fine fiber, quite indistinguishable from a real spider web, and they have the further similarity that they are just as good for catching flies.
Now, going back to the melted quartz, it is evident that if it ever became perfectly liquid, it could not exist as a fiber for an instant. It is the extreme viscosity of quartz, at the heat even of an electric arc, that makes these fibers possible. The only difference between quartz in the oxyhydrogen jet and quartz in the arc is that in the first you make threads and in the second are blown bubbles. I have in my hand some microscopic bubbles of quartz showing all the perfection of form and color that we are familiar with in the soap bubble.
An invaluable property of quartz is its power of insulating perfectly, even in an atmosphere saturated with water. The gold leaves now diverging were charged some time before the lecture, and hardly show any change, yet the insulator is a rod of quartz only three-quarters of an inch long, and the air is kept moist by a dish of water. The quartz may even be dipped in the water and replaced with the water upon it without any difference in the insulation being observed.
Not only can fibers be made of extreme fineness, but they are wonderfully uniform in diameter. So uniform are they that they perfectly stand an optical test so severe that irregularities invisible in any microscope would immediately be made apparent. Every one must have noticed when the sun is shining upon a border of flowers and shrubs how the lines which spiders use as railways to travel from place to place glisten with brilliant colors. These colors are only produced when the fibers are sufficiently fine. If you take one of these webs and examine it in the sunlight, you will find that the colors are variegated, and the effect, consequently, is one of great beauty.
A quartz fiber of about the same size shows colors in the same way, but the tint is perfectly uniform on the fiber. If the color of the fiber is examined with a prism, the spectrum is found to consist of alternate bright and dark bands. Upon the screen are photographs taken by Mr. Briscoe, a student in the laboratory at South Kensington, of the spectra of some of these fibers at different angles of incidence. It will be seen that coarse fibers have more bands than fine, and that the number increases with the angle of incidence of the light. There are peculiarities in the march of the bands as the angle increases which I cannot describe now. I may only say that they appear to move not uniformly, but in waves, presenting very much the appearance of a caterpillar walking.
So uniform are the quartz fibers that the spectrum from end to end consists of parallel bands. Occasionally a fiber is found which presents a slight irregularity here and there. A spider line is so irregular that these bands are hardly observable; but, as the photograph on the screen shows, it is possible to trace them running up and down the spectrum when you know what to look for.
To show that these longitudinal bands are due to the irregularities, I have drawn a taper piece of quartz by hand, in which the two edges make with one another an almost imperceptible angle, and the spectrum of this shows the gradual change of diameter by the very steep angle at which the bands run up the spectrum.
Into the theory of the development of these bands I am unable to enter; that is a subject on which your professor of natural philosophy is best able to speak. Perhaps I may venture to express the hope, as the experimental investigation of this subject is now rendered possible, that he may be induced to carry out a research for which he is so eminently fitted.
Though this is a subject which is altogether beyond me, I have been able to use the results in a practical way. When it is required to place into an instrument a fiber of any particular size, all that has to be done is to hold the frame of fibers toward a bright and distant light, and look at them through a low-angled prism. The banded spectra are then visible, and it is the work of a moment to pick out one with the number of bands that has been found to be given by a fiber of the desired size. A coarse fiber may have a dozen or more, while such fibers as I find most useful have only two dark bands. Much finer ones exist, showing the colors of the first order with one dark band; and fibers so fine as to correspond to the white or even the gray of Newton's scale are easily produced.
Passing now from the most scientific test of the uniformity of these fibers, I shall next refer to one more homely. It is simply this: The common garden spider, except when very young, cannot climb up one of the same size as the web on which she displays such activity. She is perfectly helpless, and slips down with a run. After vainly trying to make any headway, she finally puts her hands (or feet) into her mouth and then tries again, with no better success. I may mention that a male of the same species is able to run up one of these with the greatest ease, a feat which may perhaps save the lives of a few of these unprotected creatures when quartz fibers are more common.
It is possible to make any quantity of very fine quartz fiber without a bow and arrow at all, by simply drawing out a rod of quartz over and over again in a strong oxyhydrogen jet. Then, if a stand of any sort has been placed a few feet in front of the jet, it will be found covered with a maze of thread, of which the photograph on the screen represents a sample. This is hardly distinguishable from the web spun by this magnificent spider in corners of greenhouses and such places. By regulating the jet and the manipulation, anything from one of these stranded cables to a single ultro-microscope line may be developed.
And now that I have explained that these fibers have such valuable properties, it will no doubt be expected that I should perform some feat with their aid which, up to the present time, has been considered impossible, and this I intend to do.
Of all experiments, the one which has most excited my admiration is the famous experiment of Cavendish, of which I have a full size model before you. The object of this experiment is to weigh the earth by comparing directly the force with which it attracts things with that due to large masses of lead. As is shown by the model, any attraction which these large balls exert on the small ones will tend to deflect this 6 ft. beam in one direction, and then if the balls are reversed in position, the deflection will be in the other direction. Now, when it is considered how enormously greater the earth is than these balls, it will be evident that the attraction due to them must be in comparison excessively small. To make this evident, the enormous apparatus you see had to be constructed, and then, using a fine torsion wire, a perfectly certain but small effect was produced. The experiment, however, could only be successfully carried out in cellars and underground places, because changes of temperature produced effects greater than those due to gravity.2
Now I have in a hole in the wall an instrument no bigger than a galvanometer, of which a model is on the table. The balls of the Cavendish apparatus, weighing several hundredweight each, are replaced by balls weighing 1¾ pounds only. The smaller balls of 1¾ pounds are replaced by little weights of 15 grains each. The 6 foot beam is replaced by one that will swing round freely in a tube three-quarters of an inch in diameter. The beam is, of course, suspended by a quartz fiber. With this microscopic apparatus, not only is the very feeble attraction observable, but I can actually obtain an effect eighteen times as great as that given by the apparatus of Cavendish, and what is more important, the accuracy of observation is enormously increased.
The light from a lamp passes through a telescope lens, and falls on the mirror of the instrument. It is reflected back to the table, and thence by a fixed mirror to the scale on the wall, where it comes to a focus. If the mirror on the table were plane, the whole movement of the light would be only about eight inches, but the mirror is convex, and this magnifies the motion nearly eight times. At the present moment the attracting weights are in one extreme position, and the line of light is quiet. I will now move them to the other position, and you will see the result—the light slowly begins to move, and slowly increases in movement. In forty seconds it will have acquired its highest velocity, and in forty more it will have stopped at 5 feet 8½ inches from the starting point, after which it will slowly move back again, oscillating about its new position of rest.
It is not possible at this hour to enter into any calculations; I will only say that the motion you have seen is the effect of a force of less than one ten-millionth of the weight of a grain, and that with this apparatus I can detect a force two thousand times smaller still. There would be no difficulty even in showing the attraction between two No. 5 shot.
And now, in conclusion, I would only say that if there is anything that is good in the experiments to which I have this evening directed your attention, experiments conducted largely with sticks, and string, and straw and sealing wax, I may perhaps be pardoned if I express my conviction that in these days we are too apt to depart from the simple ways of our fathers, and instead of following them, to fall down and worship the brazen image which the instrument maker hath set up.
[1] Lecture delivered at the Royal Institution, on Friday, June 14, by Mr. C. V. Boys, F.R.S.—Nature.
[2] Dr. Lodge has been able, by an elaborate arrangement of screens, to make this attraction just evident to an audience.—C. V. B.
About HackerNoon Book Series: We bring you the most important technical, scientific, and insightful public domain books.
This book is part of the public domain. Various (2006). Scientific American Supplement, No. 717, September 28, 1889. Urbana, Illinois: Project Gutenberg. Retrieved https://www.gutenberg.org/cache/epub/17755/pg17755-images.html
This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org, located at https://www.gutenberg.org/policy/license.html.

